Chapter 1 Detection Error
Many features of kaltoa were designed specifically to deal with a common problem when positioning in acoustic telemetry arrays — reflected transmissions. That is, detections measured far later than they are expected due to not travelling the shortest path between the tag and receiver. These large outliers pose problems for synchronizing clocks and solving positions if they aren’t handled.
Rather than filtering out suspected reflected detections in preprocessing steps, kaltoa accounts for them by directly modelling them in detection error distributions. This is done by describing detection error as a mixture of a Gaussian — for direct detection error — and an approximation to a positive-valued uniform distribution — for reflected detection error. We refer to this as mixed detection error, a term that comes up frequency in kaltoa.
This mixed distribution is implemented with the ddetect function.
Here’s an example.
# Detection error values to plot
x <- seq(-0.02, 0.3, by = 0.001)
# Get mixed detection error density
y <- ddetect(x,
sigma = 0.005,# (s) Standard deviation of 0-mean Gaussian
phi = 400/1500,# (s) Upper limit of approximate uniform distribution
beta = 36# Shape parameter for the approximate uniform
)
# Plot the PDF
plot(NULL, xlim = range(x), ylim = range(y),
ylab = "Density",
xlab = "Detection error (s)",
main = "Mixed detection error")
polygon(x, y, dens = 20)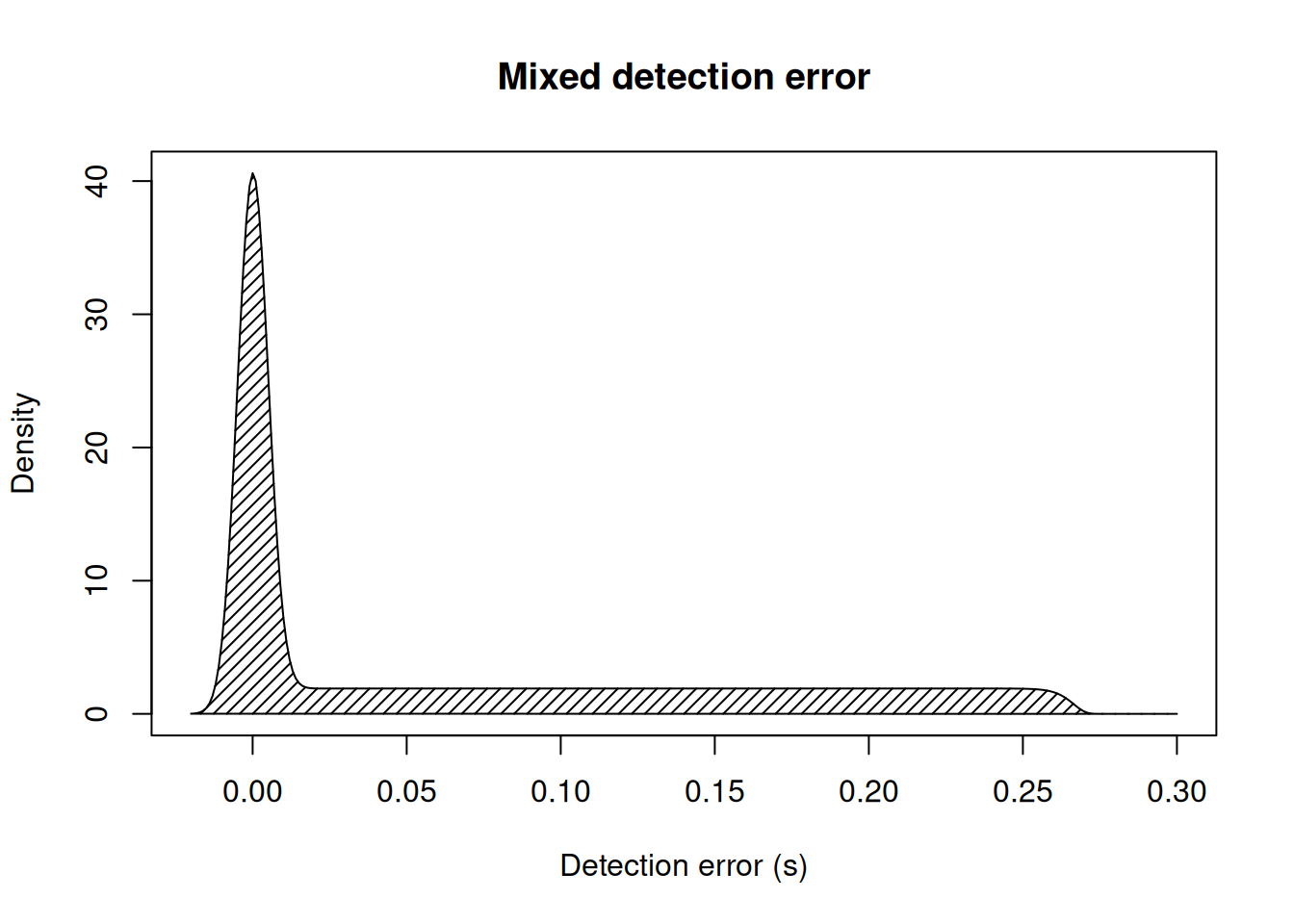
When our clocks are synchronized well and our tag sends an emission from where we expect it to be, the detection error will be 0 (the expected minus observed detection time).
Uncertainty in clock times and tag locations cause these error values to spread around that 0 mark while reflected detections cause a much greater spread of positive-only error values.
Here, we set phi = 400/1500.
The interpretation of this parameter is that reflected detections will travel and maximum additional distance of 400m before being detected.
The value of 1500 is our rough estimate for the speed of sound in water.
We assume that longer paths will result in enough transmission loss that reflected transmissions beyond that distance will no longer be detectable.
They key takeaway is that kaltoa allows for — reasonably — late arriving outliers when modelling detection error. It does not, however, allow for early arriving outliers.
For the many functions in kaltoa that make use of this error distribution, they will ask for the descriptive parameters sigma_det, phi, and beta.
You can always use the ddetect function to preview the error distribution you are passing to these functions.